APPENDIX E
Frame Variations
- xnew = x*y² - x + f(x, y, xss, yss, xs, ys)
- ynew = x²*y - y + g(x, y, xss, yss, xs, ys)
- escape = h(x, y, k)
- c = (xs, ys)
- k = iteration count
Example Frame with Pseudocode
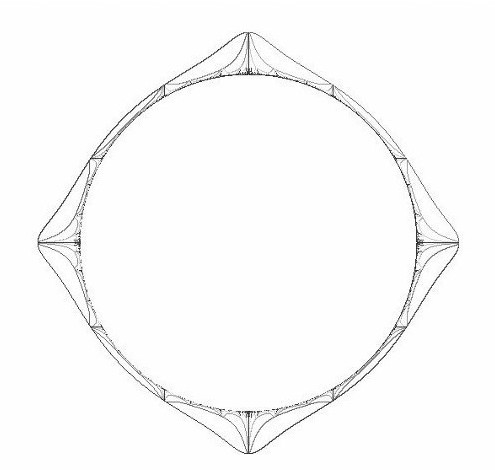
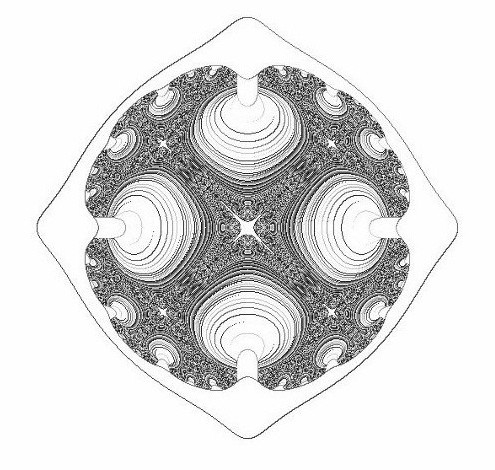
Example Frame


for (int i = 0; i ≤ 500; i++)
{
oldk = 0;
for (int j = 0; j ≤ 500; j++)
{
xs = 0.0;
ys = 0.0;
x = -2.5 + (i / 100.0);
y = -2.5 + (j / 100.0);
xss = x;
yss = y;
k = 0;
do
{
k = k + 1;
xnew = x*y*y - x + xs;
ynew = x*y*x - y + ys;
x = xnew;
y = ynew;
} while ((k ≤ kmax) && (x*x+y*y ≤ value));
if (oldk != k) PlotPixel(i, j, color));
oldk = k;
}
}
for (int j = 0; j ≤ 500; j++)
{
oldk = 0;
for (int i = 0; i ≤ 500; i++)
{ xs = 0.0;
ys = 0.0;
x = -2.5 + (i / 100.0);
y = -2.5 + (j / 100.0);
xss = x;
yss = y;
k = 0;
do
{
k = k + 1;
xnew = x*y*y - x + xs;
ynew = x*y*x - y + ys;
x = xnew;
y = ynew;
} while ((k ≤ kmax) && (x*x+y*y ≤ value));
if (oldk != k) PlotPixel(i, j, color));
oldk = k;
}
}
| Frame | Build: (f(x,y), g(x,y), c) | Escape: h(x,y) > value |
|---|---|---|
| Example (Top) | ((x*y*y - x, x*y*x - y), (0.0, 0.0)) | x*x + y*y > 6.25 |
| Example (Bottom) | ((x*y*y - x, x*y*x - y), (0.0, 0.0)) | x*x + y*y > 6.25 / k |
| Frame #1 | ((x*y*y - x + cos(xss), x*y*x - y + sin(yss)), (0.0, 0.0)) | x*x + y*y > 25.0 / k |
| Frame #2 | ((x*y*y - x + cos(xss)*cos(xss) - sin(yss)*sin(yss), x*y*x - y - 2.0*cos(xss)*sin(yss)), (0.0, 0.0)) | x*x + y*y > 16.0 / k |
| Frame #3 | ((x*y*y - x + xss*xss - yss*yss, x*y*x - y + 2.0*xss*yss)), (0.0, 0.0)) | x*x + y*y > 25.0 / k |
| Frame #4 | ((x*y*y - x + cos(xs), x*y*x - y + sin(ys)), (0.0, 0.0)) | x*x + y*y > 16.0 / k |
| Frame #5 | ((x*y*y - x + 0.5*y*y + xs, x*y*x - y + 0.5*x*x + ys), (0.0, 0.0)) | x*x + y*y > 9.0 / k |
| Frame #6 | ((x*y*y - x + cos(yss), x*y*x - y + sin(xss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #7 | ((x*y*y - x + cos(xss)*cos(xss) - sin(yss)*sin(yss), x*y*x - y + 2.0*cos(xss)*sin(yss)), (0.0, 0.0)) | x*x + y*y > 25.00 / k |
| Frame #8 | ((x*y*y - x + cos(yss)*cos(yss), x*y*x - y + sin(xss)*sin(xss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #9 | ((x*y*y - x + sin(yss), x*y*x - y + sin(xss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #10 | ((x*y*y - x + cos(yss), x*y*x - y + cos(xss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #11 | ((x*y*y - x + cos(yss + xss), x*y*x - y + cos(xss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #12 | ((x*y*y - x - x*y, x*y*x - y), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #13 | ((x*y*y - x - sin(y*y*x), x*y*x - y - sin(x*x*y)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #14 | ((x*y*y - x + sin(yss), x*y*x - y), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #15 | ((x*y*y - x - xss*xss - yss*yss, x*y*x - y + 2.0*xss*yss), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #16 | ((x*y*y - x + cos(x), x*y*x - y + sin(y)), (0.0, 0.0)) | x*x + y*y > 25.0 / k |
| Frame #17 | ((x*y*y - x + cos(x), x*y*x - y + sin(x)), (0.0, 0.0)) | x*x + y*y > 20.0 / k |
| Frame #18 | ((x*y*y - x + cos(xss), x*y*x - y + sin(xss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #19 | ((x*y*y - x - cos(xss)+sin(yss), x*y*x - y + sin(yss)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #20 | ((x*y*y - x + xss, x*y*x - y + yss), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #21 | ((x*y*y - x - xss*xss, x*y*x + y - yss*x)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #22 | ((x*y*y - x + xss*y, x*y*x + y - yss*x)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #23 | ((x*y*y - x + xss*y*yss, x*y*x + y - yss*x)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
| Frame #24 | ((x*y*y - x + x*yss, x*y*x + y - yss*x)), (0.0, 0.0)) | x*x + y*y > 20.25 / k |
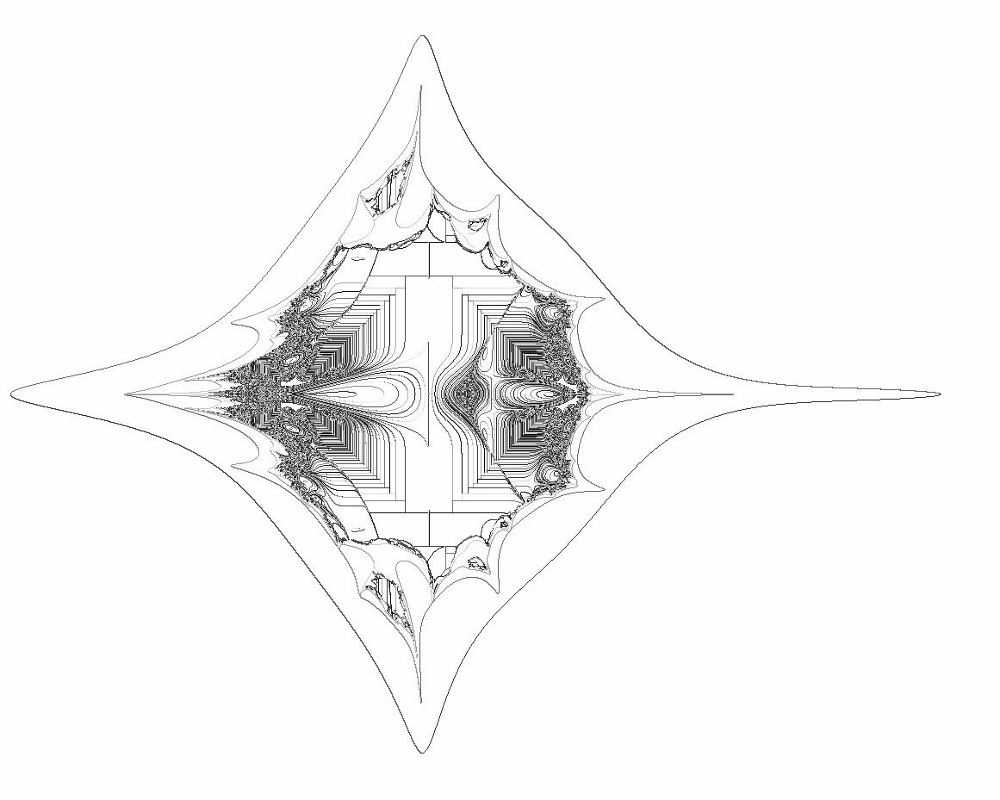
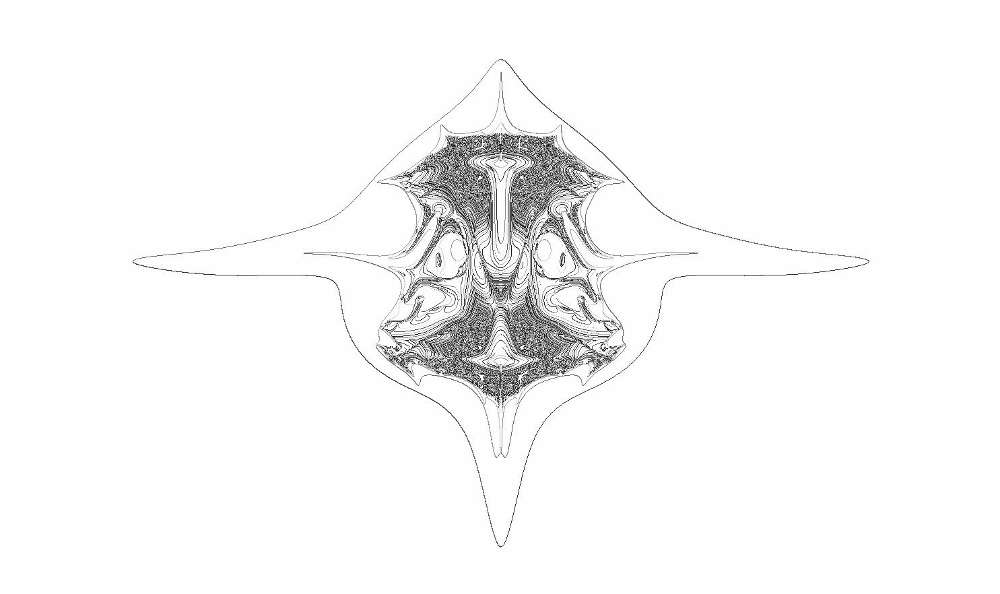










 FRACTAL FIND
FRACTAL FIND