Fractal Find : Explore Fractal and Quantum Variations

APPENDIX Q
Quantum Snowflakes

Mandelbar Variation Snowflakes use Mandelbrot variations, actually Mandelbar variations.
Mandelbrot is (x+iy)² and Mandelbar is (x-iy)² which produces a three-pronged figure.
The expression (x-iy)⁵ produces a six-pronged figure with the figure not quite radially symmetric, but with a snowflake shape.

Quantum Snowflakes use quantum sum signatures in both directions, a larger iteration limit, and a different scaling factor.

Appendix Q.A, Appendix Q.B, Appendix Q.C show all quantum snowflakes presented in Appendix A.A, Appendix A.B, Appendix A.C.

Quantum State Six-Pronged Mandelbar Snowflake with Pseudocode

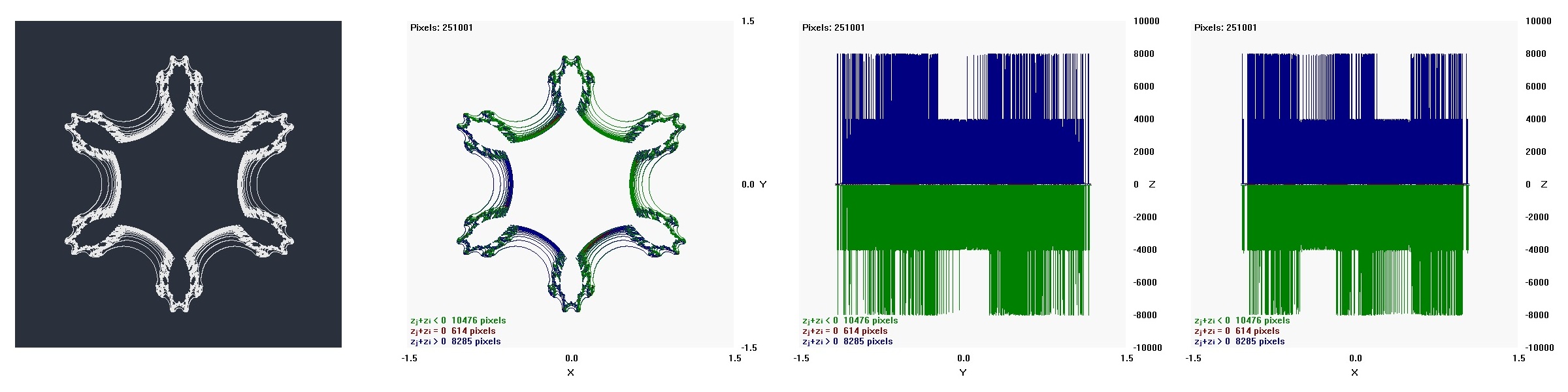
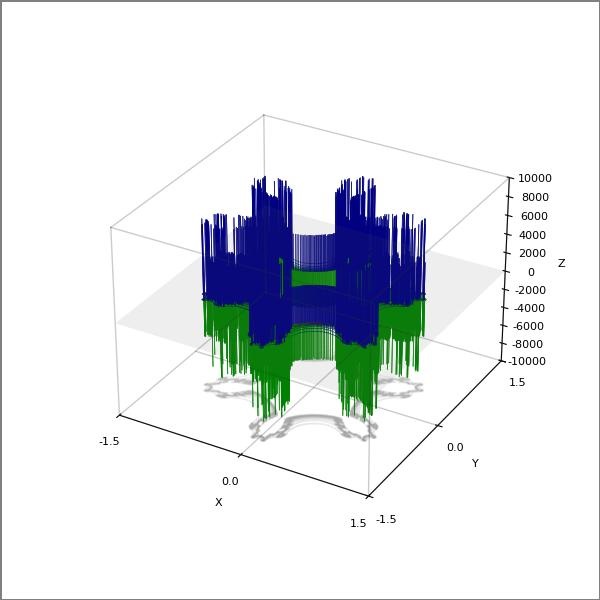
for (i = 0; i ≤ 500; i++)
{
	oldk = 0;
	for (j = 0; j ≤ 500; j++)
	{
		x = 0.0;
		y = 0.0;
		xs = -1.5+(i / 167.0);
		ys = -1.5+(j / 167.0);
		k = 0;
		do
		{
			k = k+1;
			xnew =  x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
			ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
			x = xnew;
			y = ynew;
		} while ((k ≤ 4000) && (x*x+y*y ≤ 16.0));
		if ((oldk != k) && (k > 3) && (oldk > 3)) PlotPixel(i, j, color);
		oldk = k;
	}
}
for (j = 0; j ≤ 500; j++)
{
	oldk = 0;
	for (i = 0; i ≤ 500; i++)
	{
		x = 0.0;
		y = 0.0;
		xs = -1.5+(i / 167.0);
		ys = -1.5+(j / 167.0);
		k = 0;
		do
		{
			k = k+1;
			xnew =  x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
			ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
			x = xnew;
			y = ynew;
		} while ((k ≤ 4000) && (x*x+y*y ≤ 16.0));
		if ((oldk != k) && (k > 3) && (oldk > 3)) PlotPixel(i, j, color);
		oldk = k;
	}
}

Julia Variation Snowflakes use Mandelbrot generations, actually Mandelbar generations.
The same generators are used in the Julia variations as the Mandelbar variations, but where (xs, ys) = (0, 0), the starting point.
This was an experiment, but results, in some cases, were somewhat surprising.

Quantum Snowflakes use quantum sum signatures in both directions, a larger iteration limit, and a different scaling factor.

Appendix Q.D, Appendix Q.E, Appendix Q.F show all Julia quantum variations presented in Appendix A.A, Appendix A.B, Appendix A.C.

Quantum State Julia Snowflake Variation with Pseudocode

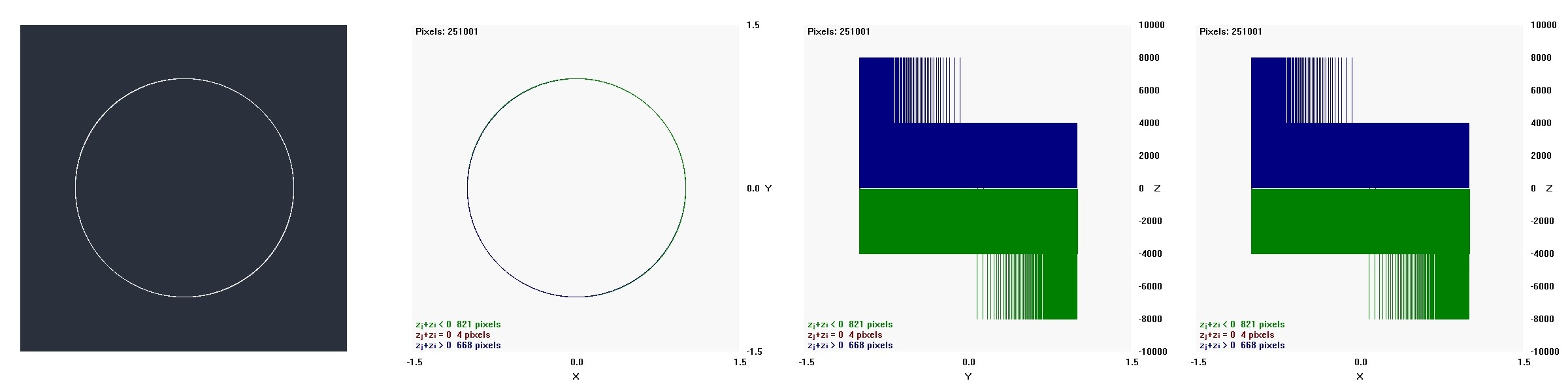
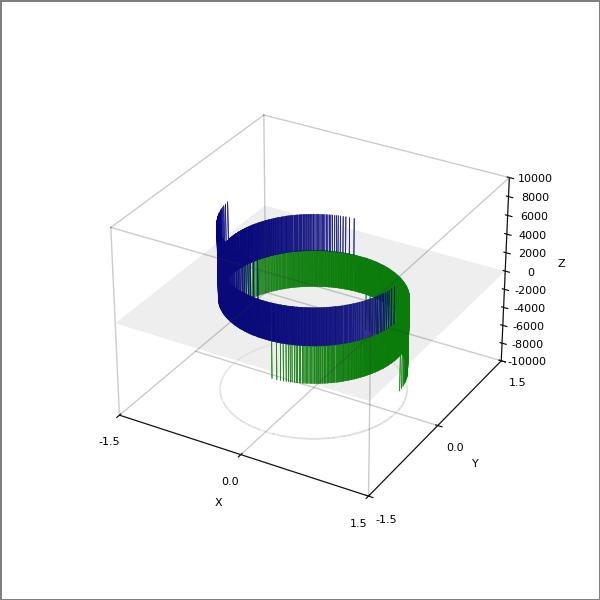
for (i = 0; i ≤ 500; i++)
{
	oldk = 0;
	for (j = 0; j ≤ 500; j++)
	{
		xs = 0.0;
		ys = 0.0;
		x = -1.5+(i / 167.0);
		y = -1.5+(j / 167.0);
		k = 0;
		do
		{
			k = k+1;
			xnew =  x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
			ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
			x = xnew;
			y = ynew;
		} while ((k ≤ 4000) && (x*x+y*y ≤ 16.0));
		if ((oldk != k) && (k > 3) && (oldk > 3)) PlotPixel(i, j, color);
		oldk = k;
	}
}
for (j = 0; j ≤ 500; j++)
{
	oldk = 0;
	for (i = 0; i ≤ 500; i++)
	{
		xs = 0.0;
		ys = 0.0;
		x = -1.5+(i / 167.0);
		y = -1.5+(j / 167.0);
		k = 0;
		do
		{
			k = k+1;
			xnew =  x⁵-10.0*x³*y²+5.0*x*y⁴+xs;
			ynew = -y⁵+10.0*x²*y³-5.0*x⁴*y+ys;
			x = xnew;
			y = ynew;
		} while ((k ≤ 4000) && (x*x+y*y ≤ 16.0));
		if ((oldk != k) && (k > 3) && (oldk > 3)) PlotPixel(i, j, color);
		oldk = k;
	}
}