Julia State Change Totals where zᵢ ≠ 0 + zⱼ ≠ 0

Section	{-}	{0}	{+}	Sum
x1,y1	0	0	1719	1719
x4,y2	0	0	8	8
x7,y3	842	44	1000	1886
x2,y4	0	0	8	8
x5,y5	0	0	0	0
x8,y6	7	0	1	8
x3,y7	842	44	1000	1886
x6,y8	7	0	1	8
x9,y9	1226	0	0	1226
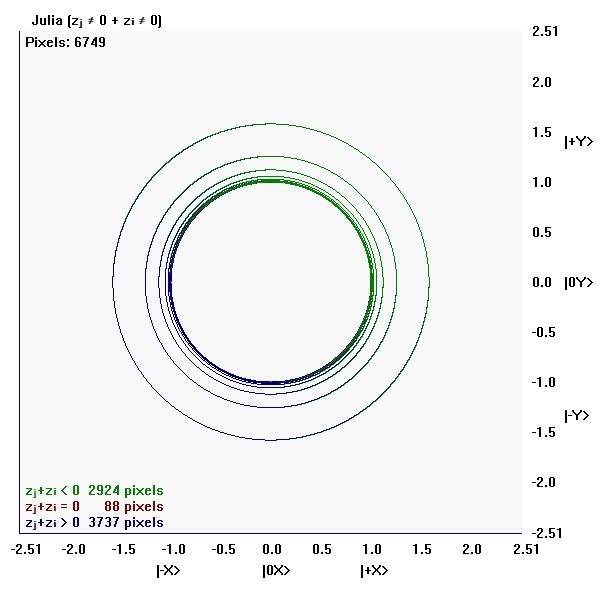
Sum	2924	88	3737	6749

Quantum Fractal Entanglement
The steps used in creating quantum Julia are the same steps used in creating quantum Mandelbrot.
See Chapter 1 for the Basic Julia Set where (xs, ys) = (0.0, 0.0) is the start point.

• zⱼ and zᵢ are calculated for the x-direction and the y-direction.
• zⱼ and zᵢ are mapped.
• zⱼ and zᵢ are summed and mapped.

Like Mandelbrot, both Julia zⱼ ≠ 0 and zᵢ ≠ 0 are necessary to provide a complete Julia map.
Julia zⱼ and zᵢ are entangled entities and the sum of both entities provides a complete map.
The three parts of the map are described and shown below:

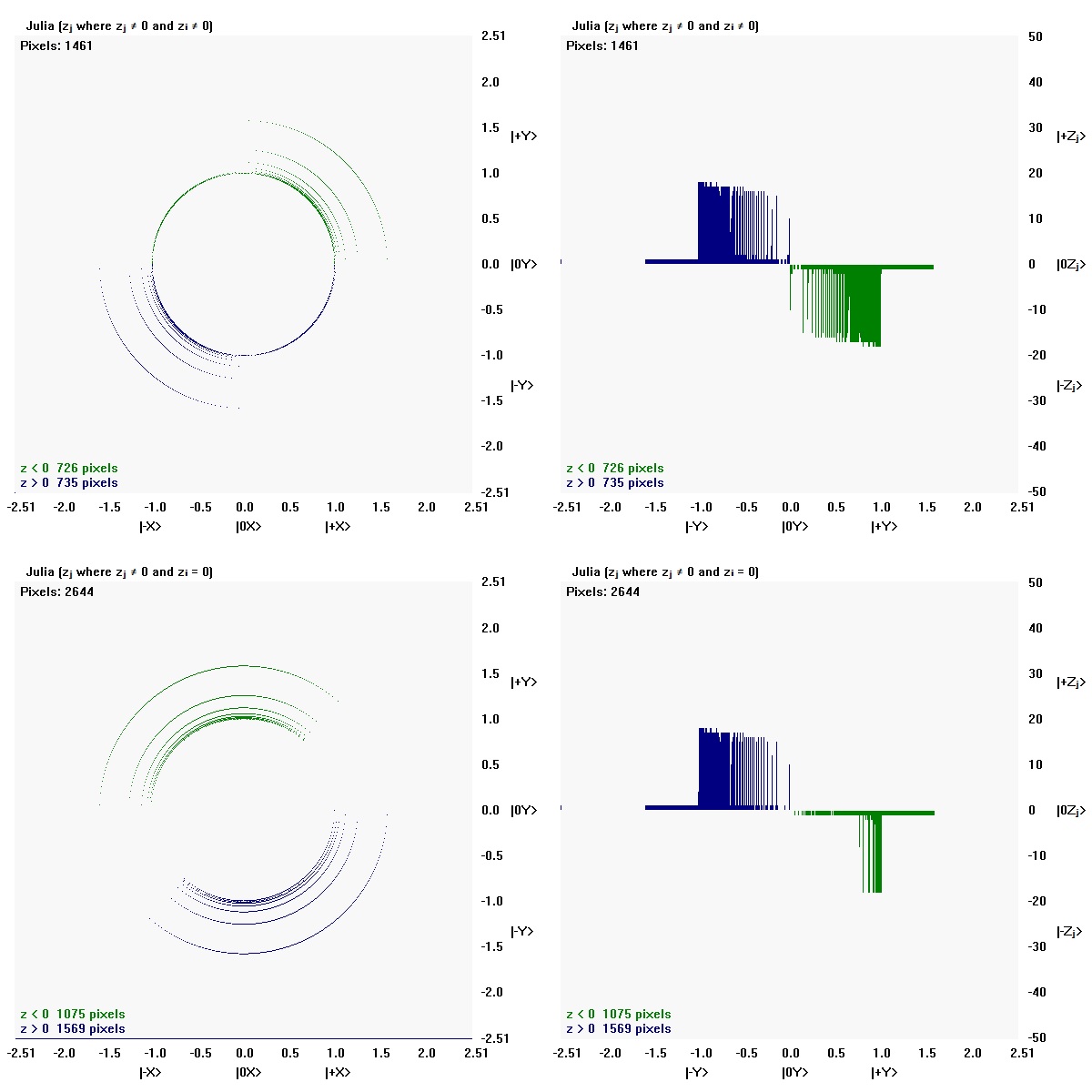
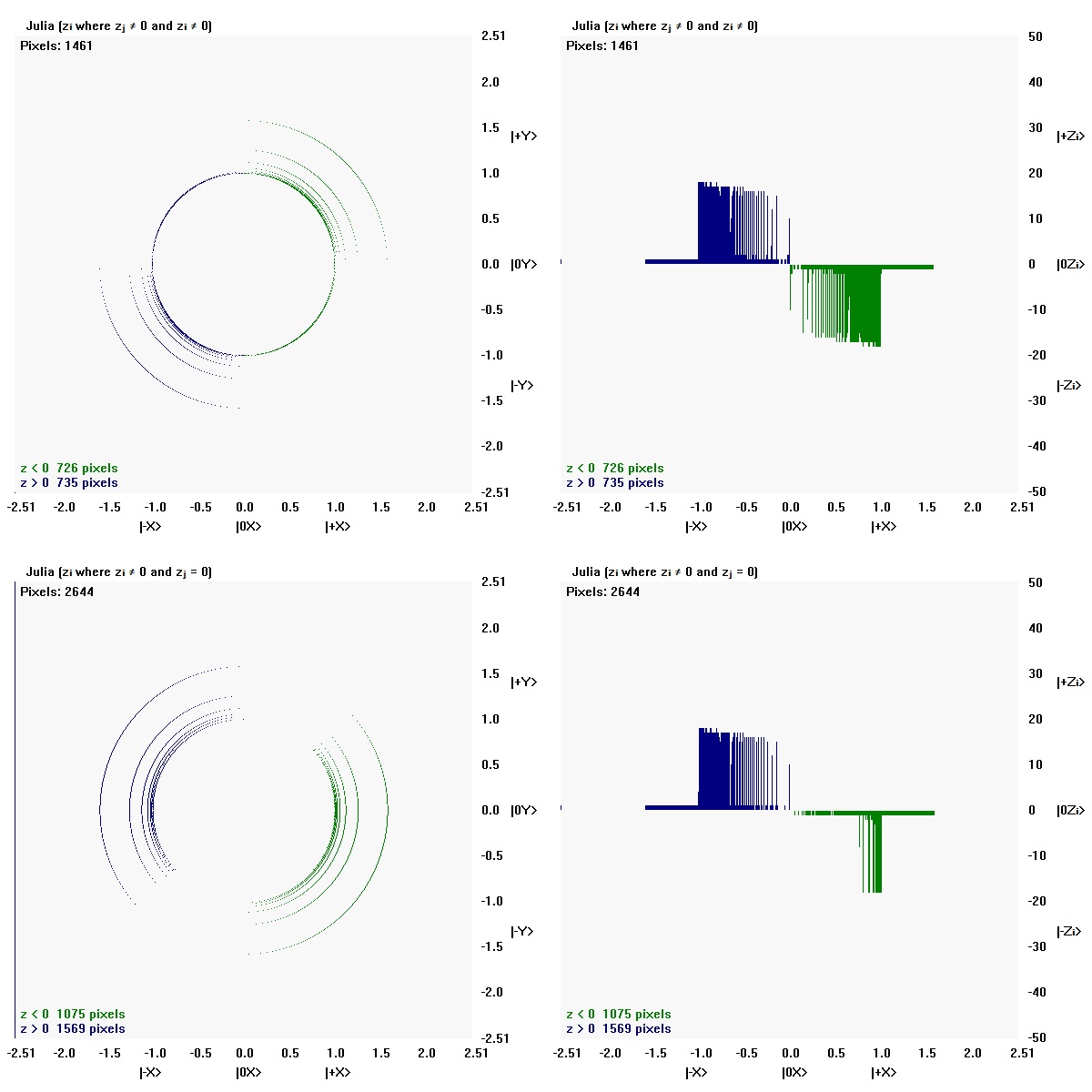
Julia (zⱼ where zⱼ ≠ 0 and zᵢ = 0)
zⱼ reflects points found only in the y-direction. There are 2644 zⱼ pixels.

Julia (zᵢ where zᵢ ≠ 0 and zⱼ = 0)
zᵢ reflects points found only in the x-direction. There are 2644 zᵢ pixels.

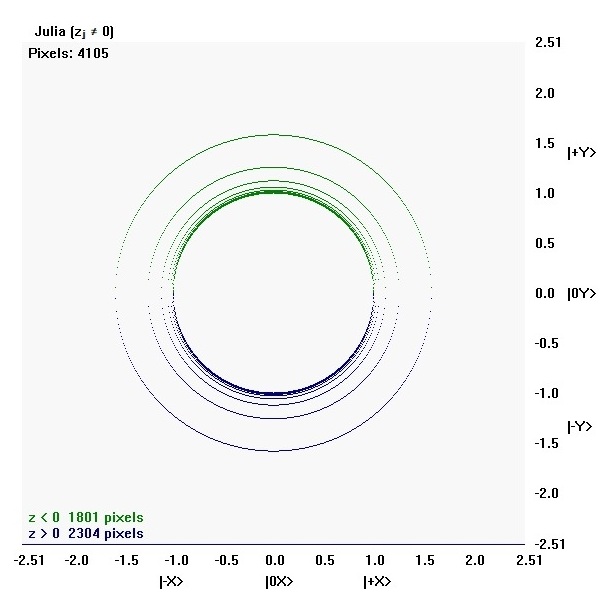
Julia (zⱼ ≠ 0 and zᵢ ≠ 0)
zⱼ ≠ 0 and zᵢ ≠ 0 reflect points in common in both the x-direction and the y-direction.
The points may be common to both zⱼ and zᵢ, but the state values are different.
There are 1461 zⱼ ≠ 0 and zᵢ ≠ 0 pixels.

To obtain the complete map, zⱼ ≠ 0, zᵢ ≠ 0 are summed yielding the map seen to the right:

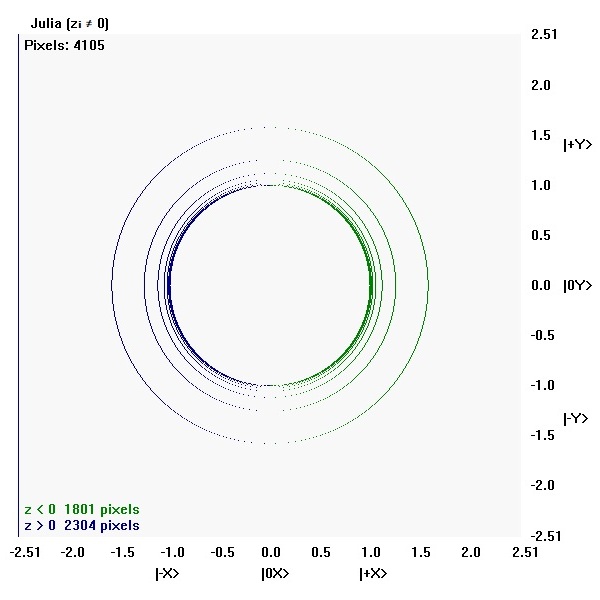
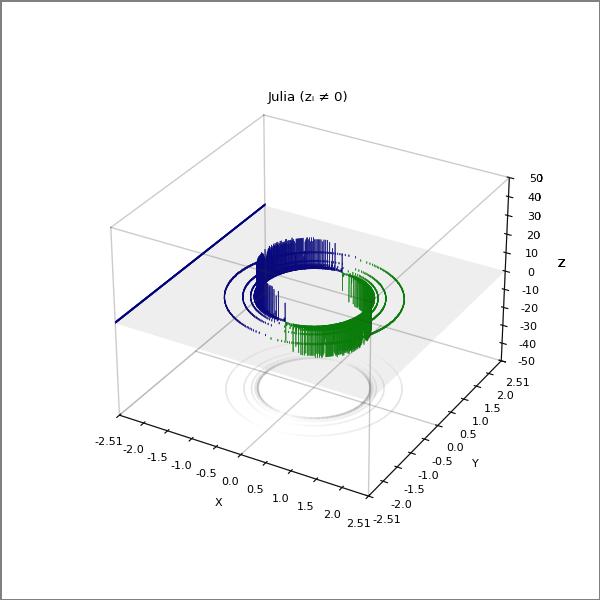
Julia (zⱼ ≠ 0 + zᵢ ≠ 0)
There are 253009 pixels in the map, but only 6749 pixels where either zⱼ ≠ 0 or zᵢ ≠ 0 or both zⱼ ≠ 0, zᵢ ≠ 0.
There are 88 pixels where zⱼ ≠ 0 and zᵢ ≠ 0, but their sum (zⱼ ≠ 0 + zᵢ ≠ 0) = 0.

Julia (zⱼ)

Julia State Change Totals (zⱼ) where zⱼ ≠ 0 and zᵢ = 0

Section	{-}	{0}	{+}	Sum
y1	0	0	572	572
y2	0	0	0	0
y3	739	0	0	739
y4	0	0	7	7
y5	0	0	0	0
y6	7	0	0	7
y7	0	0	989	989
y8	0	0	1	1
y9	329	0	0	329
Sum	1075	0	1569	2644

Julia State Change Totals (zⱼ) where zⱼ ≠ 0 and zᵢ ≠ 0

Section	{-}	{0}	{+}	Sum
y1	0	0	575	575
y2	0	0	1	1
y3	158	0	0	158
y4	0	0	1	1
y5	0	0	0	0
y6	0	0	0	0
y7	0	0	158	158
y8	0	0	0	0
y9	568	0	0	568
Sum	726	0	735	1461