CHAPTER 11
Fractal-Lorenz Map
A Fractal-Lorenz Map is a combination of a fractal figure and Lorenz calculations.
On the left-hand side, the Mandelbrot pixel and point figures are presented and pseudocode is shown.
One hundred iterations of the Mandelbrot-Lorenz Map were generated with the map plotted each ten iterations.
On the right-hand side, the Mandelbrot-Lorenz Map at 40 iterations is presented (X-Y, X-Z, Y-Z respectively) and pseudocode is shown where:
- dt=0.02
- r=28.0
- s=10.0
- b=2.667

Mandelbrot Pixel and Point
for (int i = 0; i ≤ 500; i++)
{
for (int j = 0; j ≤ 500; j++)
{
x = 0.0;
y = 0.0;
xs = -2.5 + (i / 100.0);
ys = -2.5 + (j / 100.0);
k = 0;
do
{
xnew = x*x - y*y + xs;
ynew = 2.0*x*y + ys;
x = xnew;
y = ynew;
k = k + 1;
} while ((k ≤ 64) && (x*x + y*y ≤ 6.25));
xarray[i][j] = x;
yarray[i][j] = y;
zarray[i][j] = k;
PlotPixel(i, j, color);
PlotPoint(x, y, color);
}
}
Mandelbrot-Lorenz Map
for (int m = 1; m ≤ 100; m++)
{
for (int i = 0; i ≤ 500; i++)
{
for (int j = 0; j ≤ 500; j++)
{
x = xarray[i][j];
y = yarray[i][j];
z = zarray[i][j];
dx = s * (y - x);
dy = r * x - y - x * z;
dz = x * y - b * z;
xarray[i][j] = x = x + dx * dt;
yarray[i][j] = y = y + dy * dt;
zarray[i][j] = z = z + dz * dt;
if (m % 10 == 0)
{
PlotPoint(x, y, color);
PlotPoint(x, z, color);
PlotPoint(y, z, color);
}
}
}
}
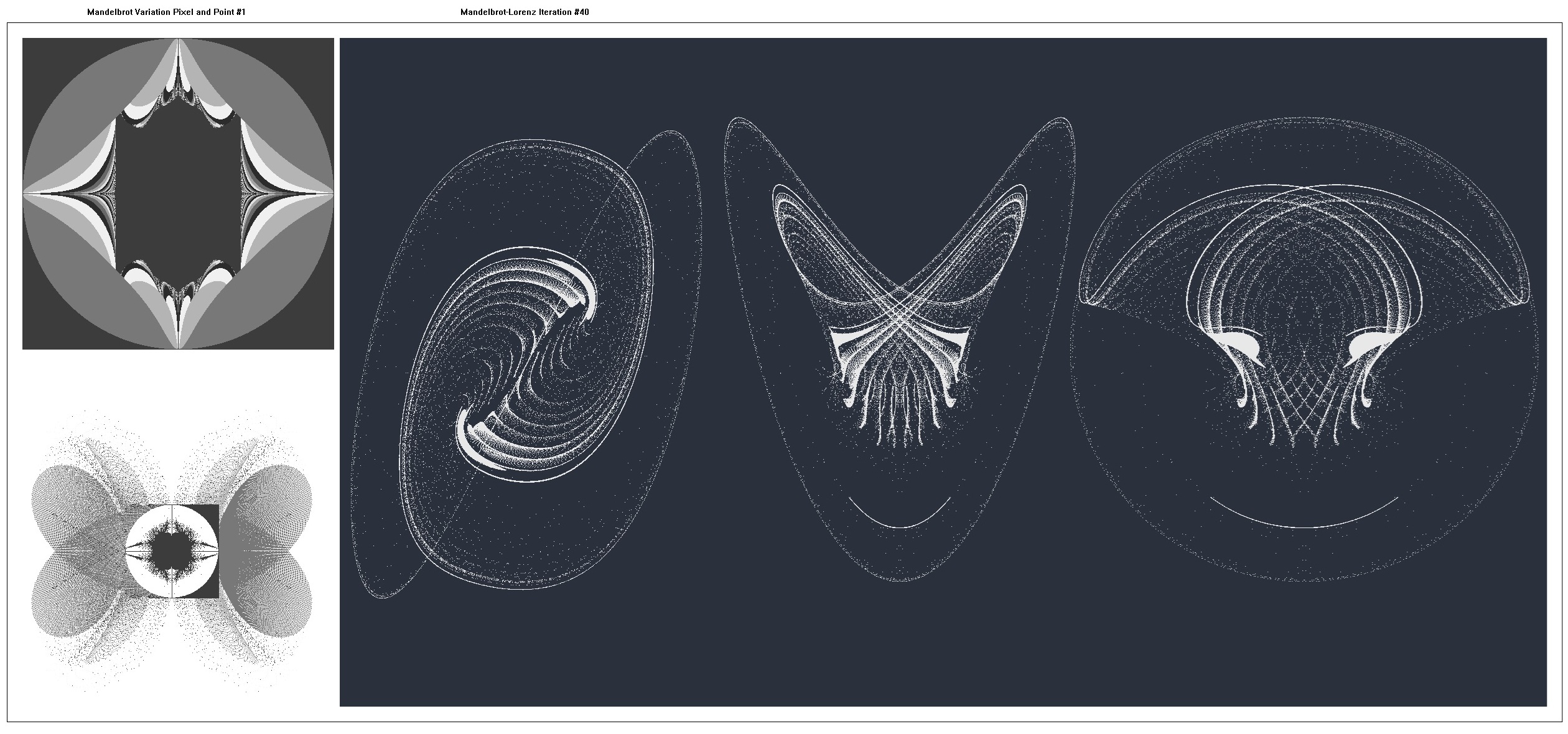
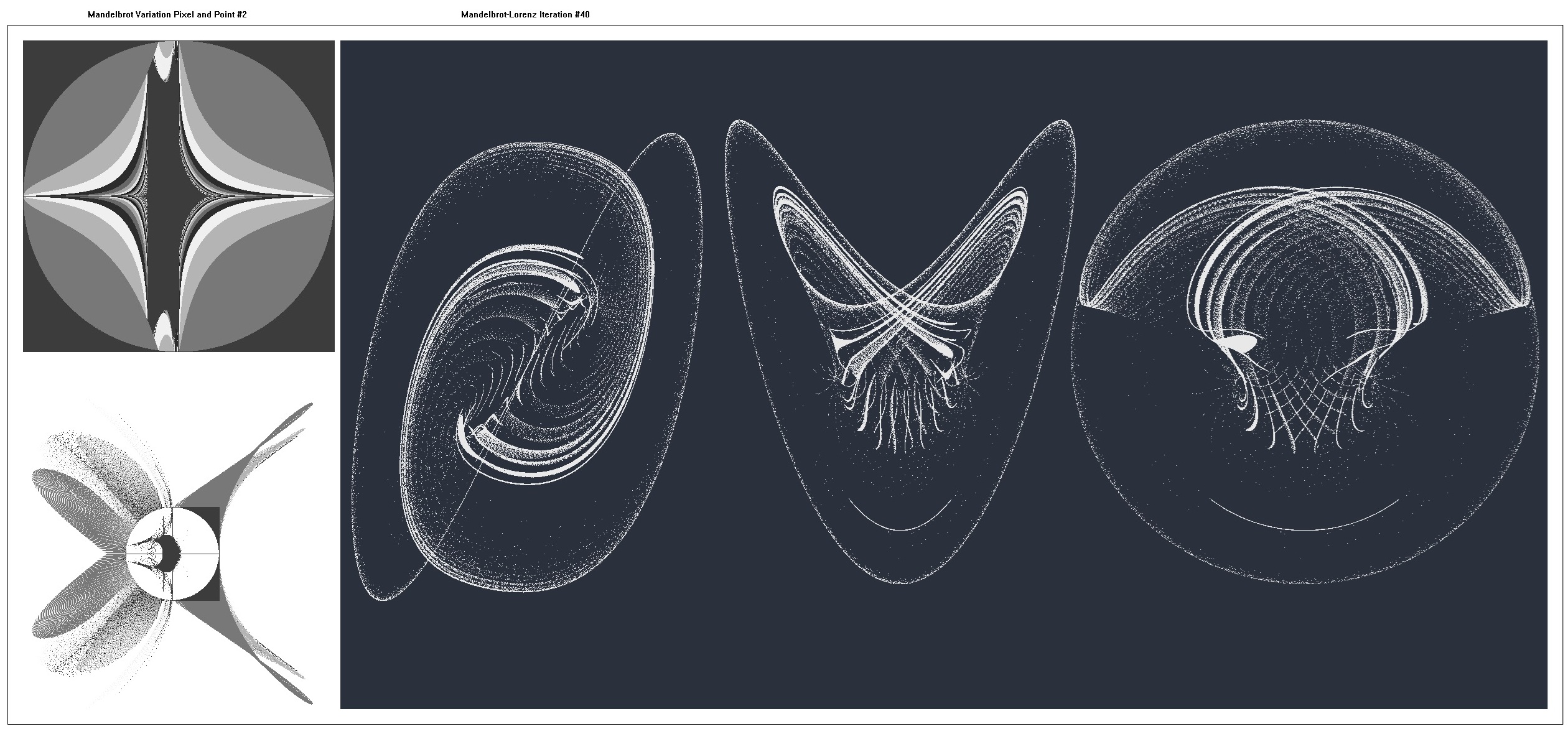
| Mandelbrot | Build: (f(x,y), g(x,y)) | Escape: h(x,y)>value | Plot |
|---|---|---|---|
| Basic Mandelbrot Set | (x² - y², 2.0*x*y) | x² + y² > 6.25 | Pixel, Point, Lorenz |
| Mandelbrot Variant #1 | (x*y², -y*x²) | x³ + y² > 6.25 | Pixel, Point, Lorenz |
| Mandelbrot Variant #2 | (x*y², 2.0*x*y) | x³ + y² > 6.25 | Pixel, Point, Lorenz |
On the left-hand side, the Julia pixel and point figures are presented and pseudocode is shown.
One hundred iterations of the Julia-Lorenz Map were generated with the map plotted each ten iterations.
On the right-hand side, the Julia-Lorenz Map at 40 iterations is presented (X-Y, X-Z, Y-Z respectively) and pseudocode is shown where:
- dt=0.02
- r=28.0
- s=10.0
- b=2.667

Julia Pixel and Point
for (int i = 0; i ≤ 500; i++)
{
for (int j = 0; j ≤ 500; j++)
{
xs = 0.0;
ys = 0.0;
x = -2.5 + (i / 100.0);
y = -2.5 + (j / 100.0);
k = 0;
do
{
xnew = x*x - y*y + xs;
ynew = 2.0*x*y + ys;
x = xnew;
y = ynew;
k = k + 1;
} while ((k ≤ 64) && (x*x + y*y ≤ 6.25));
xarray[i][j] = x;
yarray[i][j] = y;
zarray[i][j] = k;
PlotPixel(i, j, color);
PlotPoint(x, y, color);
}
}
Julia-Lorenz Map
for (int m = 1; m ≤ 100; m++)
{
for (int i = 0; i ≤ 500; i++)
{
for (int j = 0; j ≤ 500; j++)
{
x = xarray[i][j];
y = yarray[i][j];
z = zarray[i][j];
dx = s * (y - x);
dy = r * x - y - x * z;
dz = x * y - b * z;
xarray[i][j] = x = x + dx * dt;
yarray[i][j] = y = y + dy * dt;
zarray[i][j] = z = z + dz * dt;
if (m % 10 == 0)
{
PlotPoint(x, y, color);
PlotPoint(x, z, color);
PlotPoint(y, z, color);
}
}
}
}
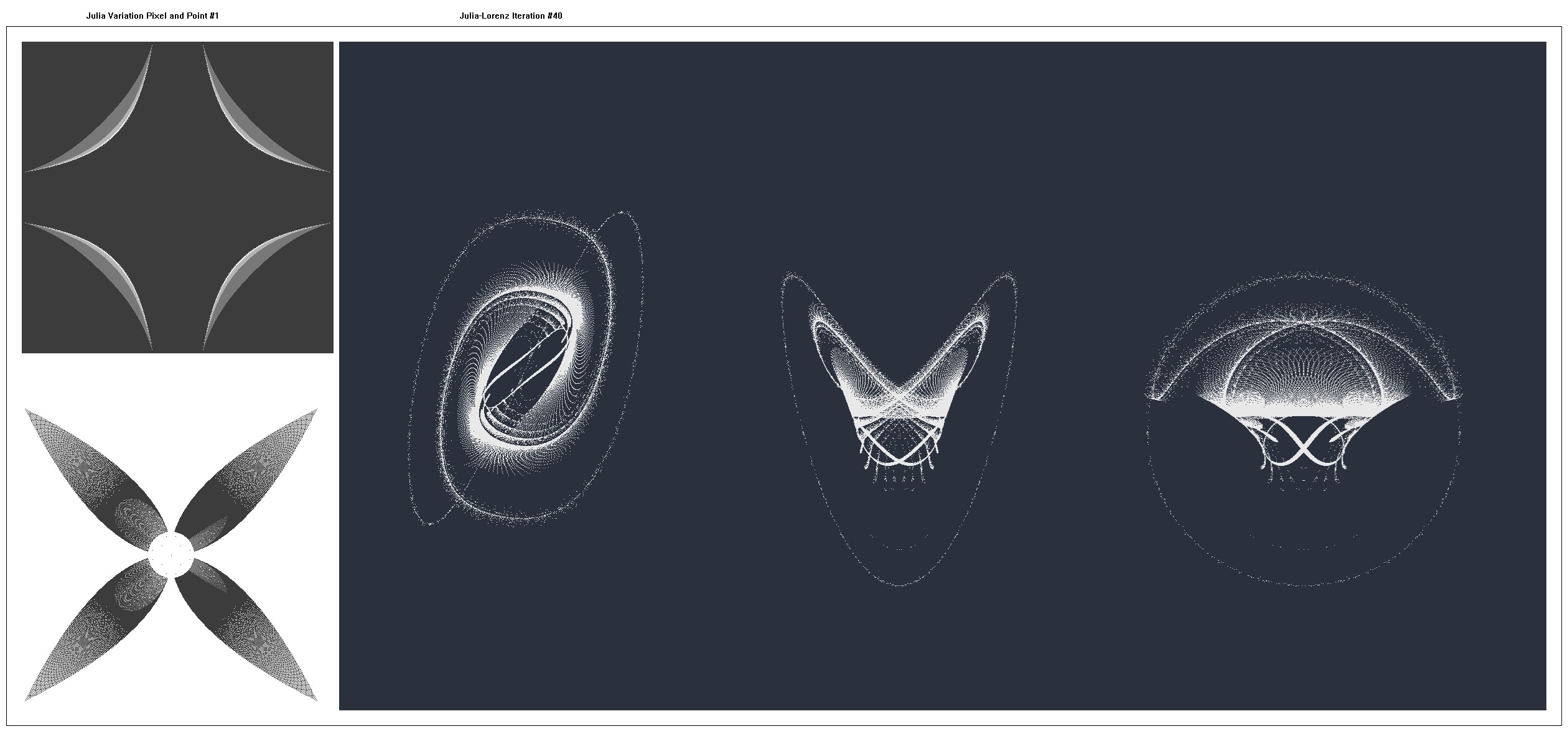
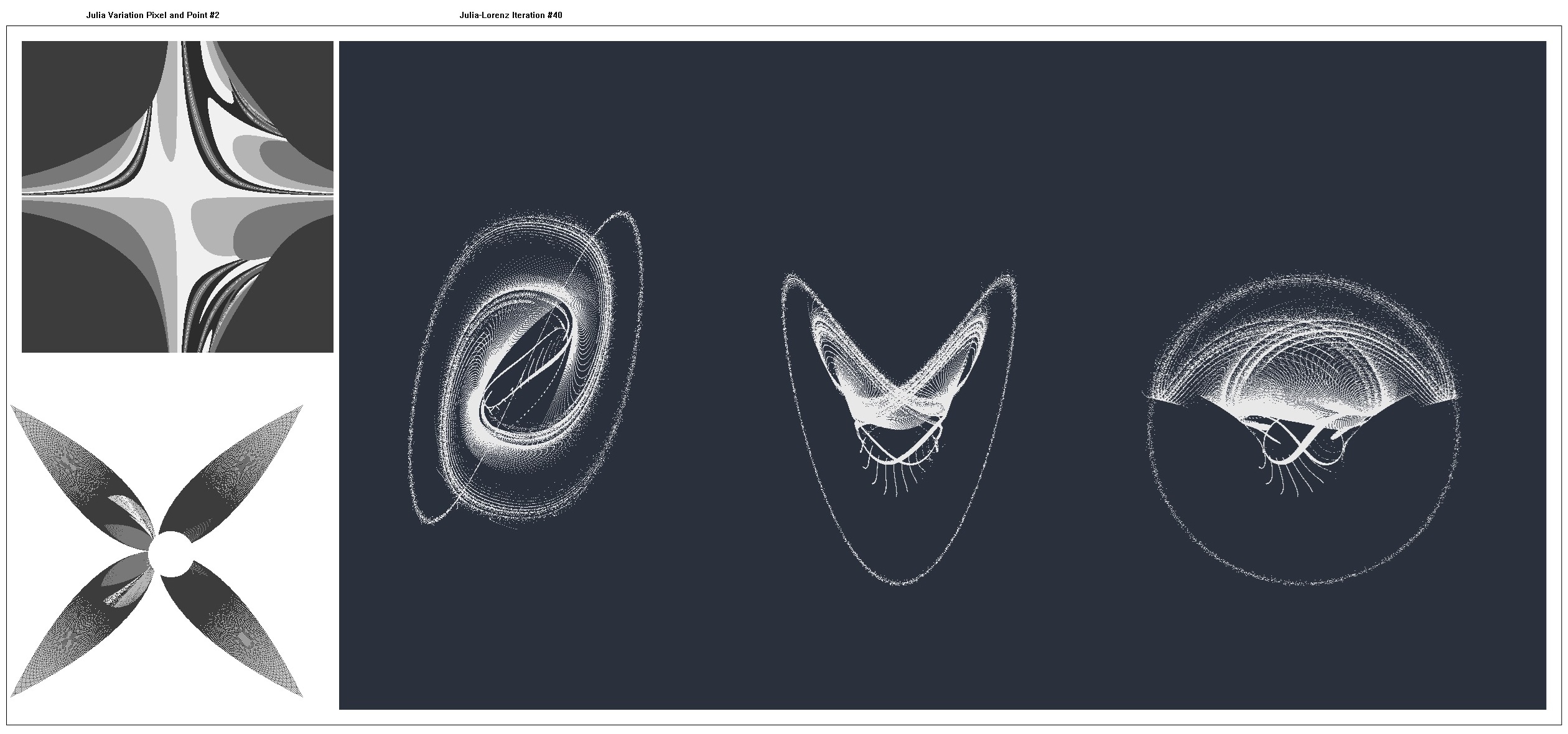
| Julia | Build: (f(x, y), g(x, y), (xs, ys)) | Escape: h(x, y)>value | Plot |
|---|---|---|---|
| Basic Julia Set (0.0, 0.0) | (x² - y², 2.0*x*y), (0.0, 0.0) | x² + y² > 6.25 | Pixel, Point, Lorenz |
| Julia Variant #1 | (x*y², -y*x²), (0.0, 0.0) | x² + y² > 6.25 | Pixel, Point, Lorenz |
| Julia Variant #2 | (x*y², -y*x²), (-1.540, 0.320) | x² + y² > 6.25 | Pixel, Point, Lorenz |
Resource for Lorenz calculations:
https://en.wikipedia.org/wiki/Lorenz_system
 FRACTAL FIND
FRACTAL FIND