CHAPTER 6
Fractal Fold Variations
Trigonometric functions create folds.
Both the Mandelbrot fold figures and the Julia fold figures use pixel dimensions that are increased by 100 pixels in both the x-direction and the y-direction for each figure.
When the pixel dimension is increased, the number of folds also increases.
 Mandelbrot Point showing Folds Example
Mandelbrot Point showing Folds Example
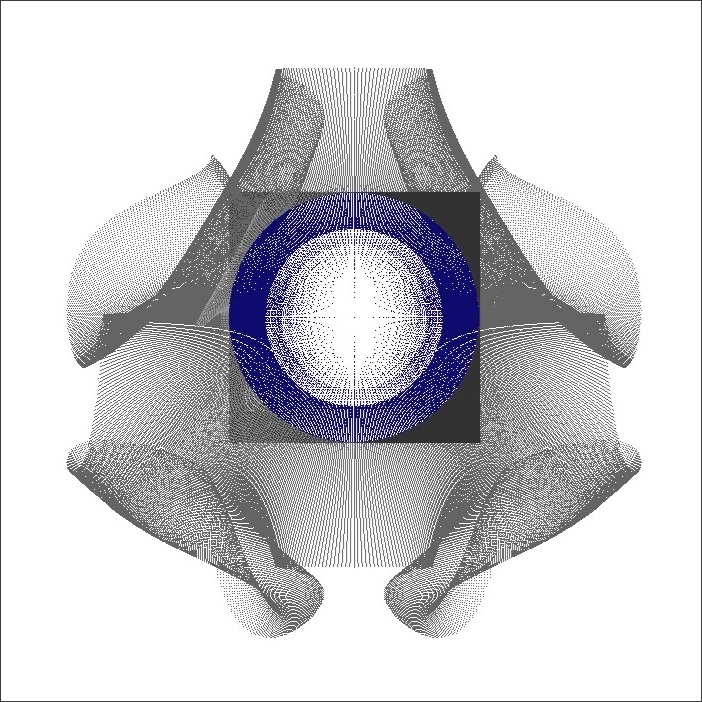
- Build: (x+sin(y*x*y)+xs, y+cos(x*x*y)-1.0+ys)
- Escape: x²+y² > (2.5+m/2.0)²/k
for (int m = 0; m ≤ 4; m++)
{
for (int i = 0; i ≤ 500+m*100; i++)
{
for (int j = 0; j ≤ 500+m*100; j++)
{
x = 0.0;
y = 0.0;
xs = -2.5 - m/2.0 + (i/100.0);
ys = -2.5 - m/2.0 + (j/100.0);
k = 0;
do
{
xnew = x + sin(y*x*y) + xs;
ynew = y + cos(x*x*y) - 1.0 + ys;
x = xnew;
y = ynew;
k = k + 1;
} while ((k ≤ kmax) && (x²+y² ≤ (2.5+m/2.0)²/k));
color = gray;
if (x²+y² ≤ (2.5+m/2.0)²) color = blue;
PlotPixel(i, j, color);
PlotPoint(x, y, color);
}
}
}
See Appendix F for additional fold (Seashell) figures.
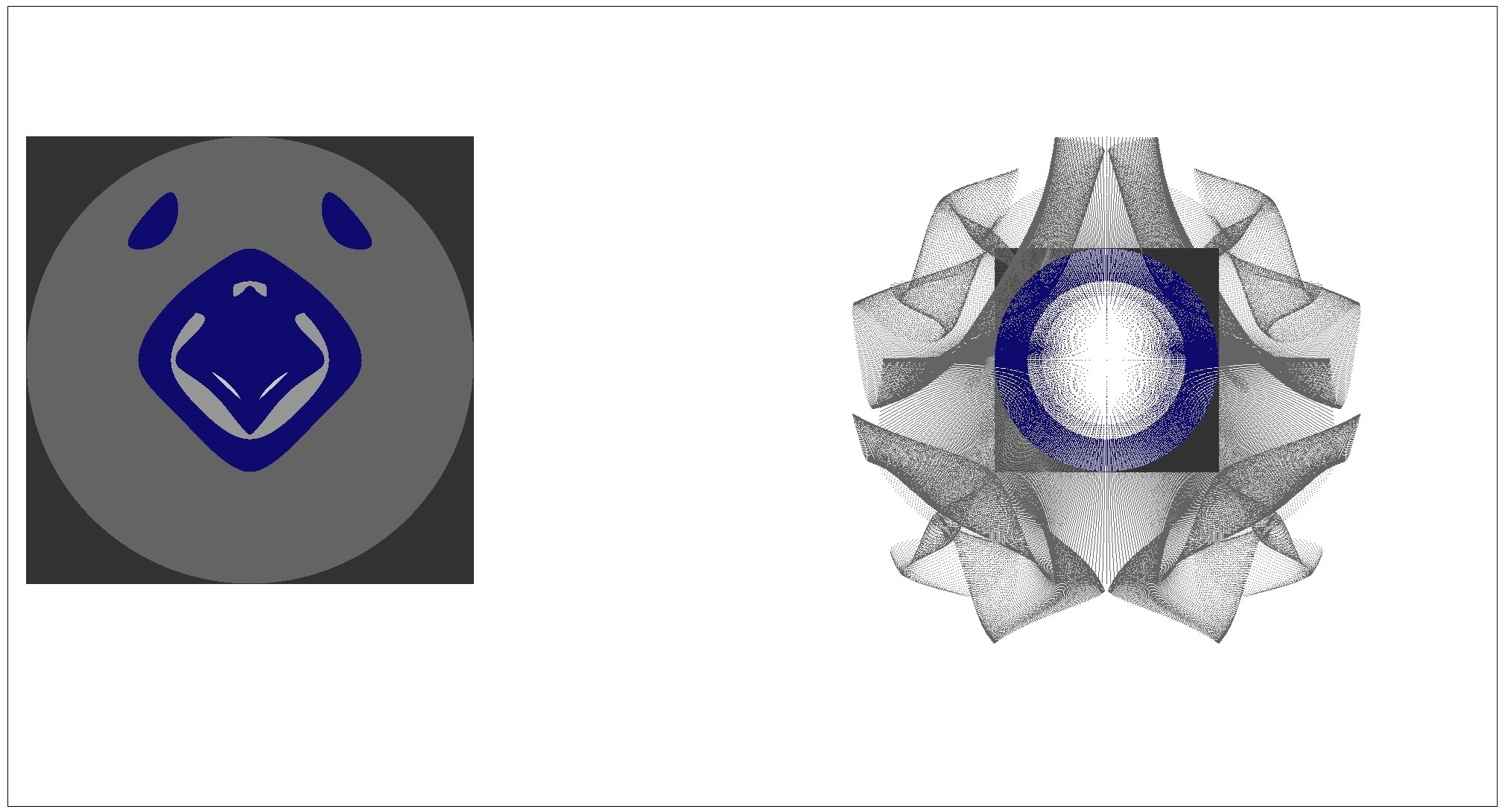
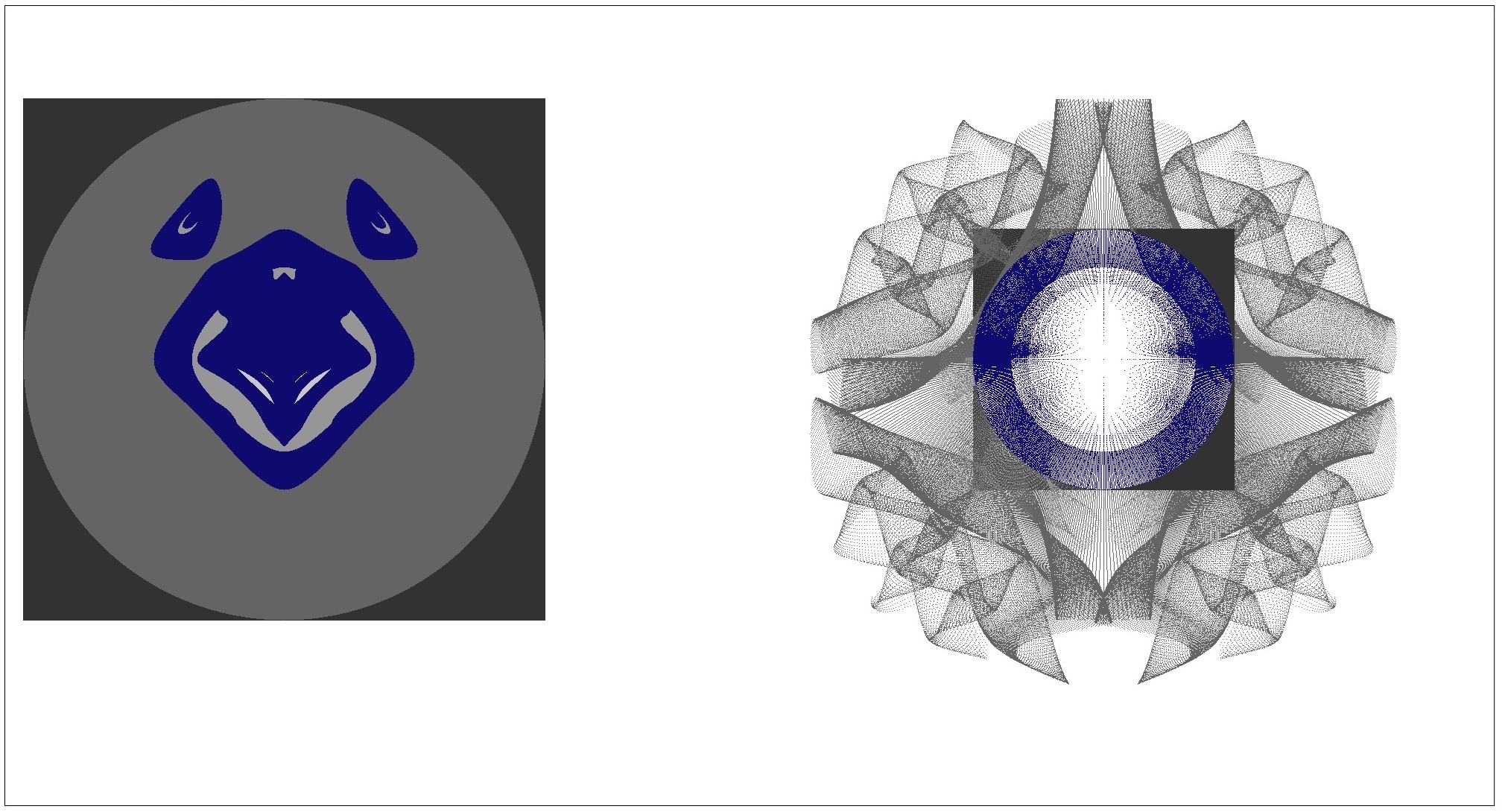


 Julia Point showing Folds Example
Julia Point showing Folds Example

- Build: (x+sin(y*x*y)+xs, y+cos(x*x*y)-1.0+ys, (0.0, 0.0))
- Escape: x²+y² > (2.5+m/2.0)²/k
for (int m = 0; m ≤ 4; m++)
{
for (int i = 0; i ≤ 500+m*100; i++)
{
for (int j = 0; j ≤ 500+m*100; j++)
{
xs = 0.0;
ys = 0.0;
x = -2.5 - m/2.0 + (i/100.0);
y = -2.5 - m/2.0 + (j/100.0);
k = 0;
do
{
xnew = x + sin(y*x*y) + xs;
ynew = y + cos(x*x*y) - 1.0 + ys;
x = xnew;
y = ynew;
k = k + 1;
} while ((k ≤ kmax) && (x²+y² ≤ (2.5+m/2.0)²/k));
color = gray;
if (x²+y² ≤ (2.5+m/2.0)²) color = blue;
PlotPixel(i, j, color);
PlotPoint(x, y, color);
}
}
}




 FRACTAL FIND
FRACTAL FIND