Under what circumstances do fractal figures remain recognizable with modifications?

How sensitive are fractal figures to change?

Is it possible to determine the fractal generator from the figure?

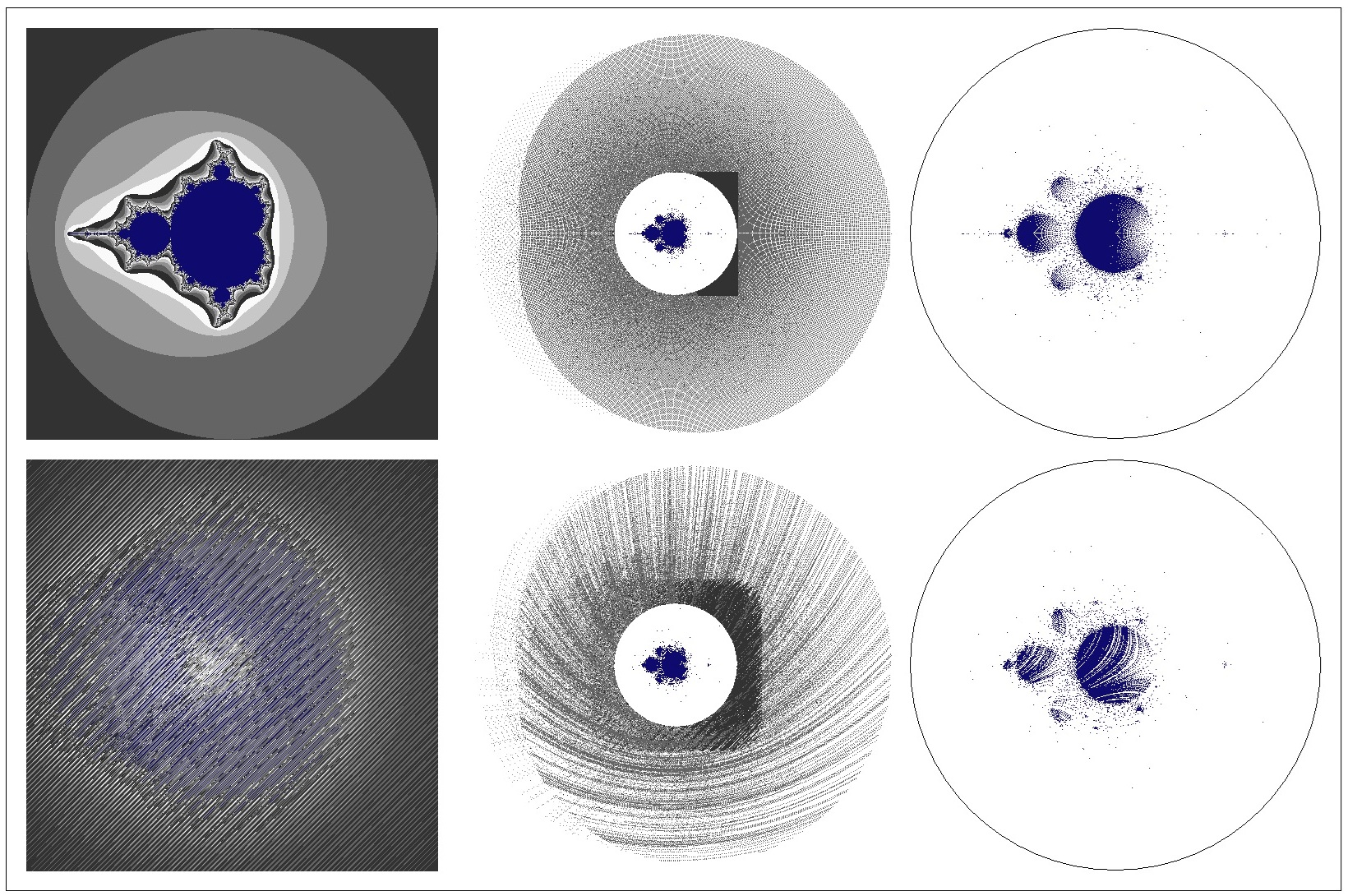
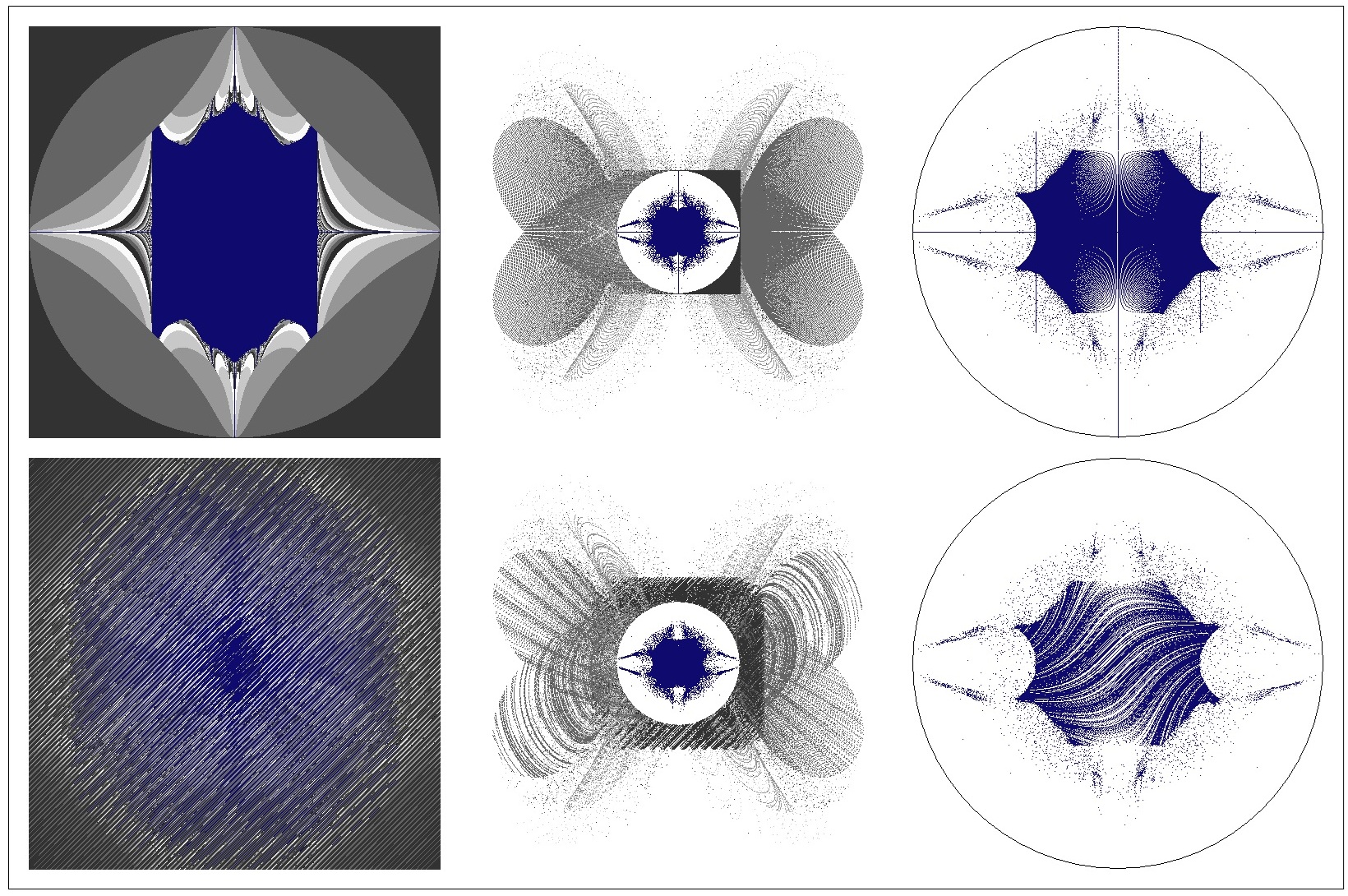
The top Mandelbrot figures and Julia figures (pixel, point, center points) are clearly recognizable as basic shapes.
The bottom left Mandelbrot or Julia figure (pixel) is unrecognizable, while the bottom right Mandelbrot or Julia figures (point, center points) retain basic shapes.

See Chapter 1, Chapter 2, Chapter 3, and Chapter 6 for information on Mandelbrot Sets and Julia Sets.

Basic Mandelbrot Set Configuration

Basic Mandelbrot Set with Pseudocode

for (int i = 0; i ≤ 500; i++)
{
	for (int j = 0; j ≤ 500; j++)
	{
		x = 0.0;
		y = 0.0;
		xs = -2.5 + (i / 100.0);
		ys = -2.5 + (j / 100.0);
		k = 0;
		do
		{
Top			xnew = x * x - y * y + xs;
Top			ynew = 2.0 * x * y + ys;
Bottom		        xnew = sin(i - j) + x * x - y * y + xs;
Bottom		        ynew = cos(i - j) + 2.0 * x * y + ys;
			x = xnew;
			y = ynew;
			k = k + 1;
		} while ((k ≤ 64) && (x * x + y * y ≤ 6.25));
		color = gray;
		if (x * x + y * y ≤ 6.25) color = blue;
		PlotPixel(i, j, color);
		PlotPoint(x, y, color);
		PlotCenterPoints(x, y, color);
	}
}

Mandelbrot Variant #1

Mandelbrot Variant #2

Mandelbrot	Build: (f(x,y), g(x,y))	Escape: h(x,y)>value	Plot
Basic Mandelbrot Set Top	(x² - y², 2.0*x*y)	x² + y² > 6.25	Pixel, Point, Center
Basic Mandelbrot Set Bottom	(x² - y² + sin(i-j), 2.0*x*y + cos(i-j))	x² + y² > 6.25	Pixel, Point, Center
Mandelbrot Variant #1 Top	(x*y², -y*x²)	x³ + y² > 6.25	Pixel, Point, Center
Mandelbrot Variant #1 Bottom	(x*y² + sin(i-j), -y*x² + cos(i-j))	x³ + y² > 6.25	Pixel, Point, Center
Mandelbrot Variant #2 Top	(sin(y*x²) + x, y + sin(x*y² + x))	x³ + y² > 6.25/(k*k*k)	Pixel, Point, Center
Mandelbrot Variant #2 Bottom	(sin(i-j) + sin(y*x²) + x, y + sin(x*y² + x))	x³ + y² > 6.25/(k*k*k)	Pixel, Point, Center

Basic Julia Set Configuration

Basic Julia Set with Pseudocode

for (int i = 0; i ≤ 500; i++)
{
	for (int j = 0; j ≤ 500; j++)
	{
		xs = 0.0;
		ys = 0.0;
		x = -2.5 + (i / 100.0);
		y = -2.5 + (j / 100.0);
		k = 0;
		do
		{
Top			xnew = x * x - y * y + xs;
Top			ynew = 2.0 * x * y + ys;
Bottom		        xnew = sin(i - j) + x * x - y * y + xs;
Bottom		        ynew = cos(i - j) + 2.0 * x * y + ys;
			x = xnew;
			y = ynew;
			k = k + 1;
		} while ((k ≤ 64) && (x * x + y * y ≤ 6.25));
		color = gray;
		if (x * x + y * y ≤ 6.25) color = blue;
		PlotPixel(i, j, color);
		PlotPoint(x, y, color);
		PlotCenterPoints(x, y, color);

    }
}

Julia Variant #1

Julia Variant #2

Julia	Build: (f(x, y), g(x, y), (xs, ys))	Escape: h(x, y)>value	Plot
Basic Julia Set (0.0, 0.0) Top	(x² - y², 2.0*x*y), (0.0, 0.0)	x² + y² > 6.25	Pixel, Point, Center
Basic Julia Set (0.0, 0.0) Bottom	(x² - y² + sin(i-j), 2.0*x*y + cos(i-j)), (0.0, 0.0)	x² + y² > 6.25	Pixel, Point, Center
Julia Variant #1 Top	(x*y², -y*x²), (0.0, 0.0)	x² + y² > 6.25	Pixel, Point, Center
Julia Variant #1 Bottom	(x*y² + sin(i-j), -y*x² + cos(i-j)), (0.0, 0.0)	x² + y² > 6.25	Pixel, Point, Center
Julia Variant #2 Top	(sin(x²*y) + x, y + sin(x*y² + x)), (0.0, 0.0)	x² + y² > 6.25/(k*k*k)	Pixel, Point, Center
Julia Variant #2 Bottom	(sin(i-j) + sin(x²*y) + x, y + sin(x*y² + x)), (0.0, 0.0)	x² + y² > 6.25/(k*k*k)	Pixel, Point, Center