Mandelbrot State Change Totals where zᵢ ≠ 0 + zⱼ ≠ 0

Section	{-}	{0}	{+}	Sum
x1,y1	601	199	3721	4521
x4,y2	0	0	60	60
x7,y3	2796	144	2118	5058
x2,y4	22	1	21	44
x5,y5	0	0	0	0
x8,y6	33	1	9	43
x3,y7	1367	37	1201	2605
x6,y8	16	0	1	17
x9,y9	1711	49	194	1954
Sum	6546	431	7435	14302

Quantum Fractal Entanglement
Both Mandelbrot zⱼ ≠ 0 and zᵢ ≠ 0 are necessary to provide a complete Mandelbrot map.
Mandlebrot zⱼ and zᵢ are entangled entities and the sum of both entities provides a complete map. The three parts of the map are described and shown below:

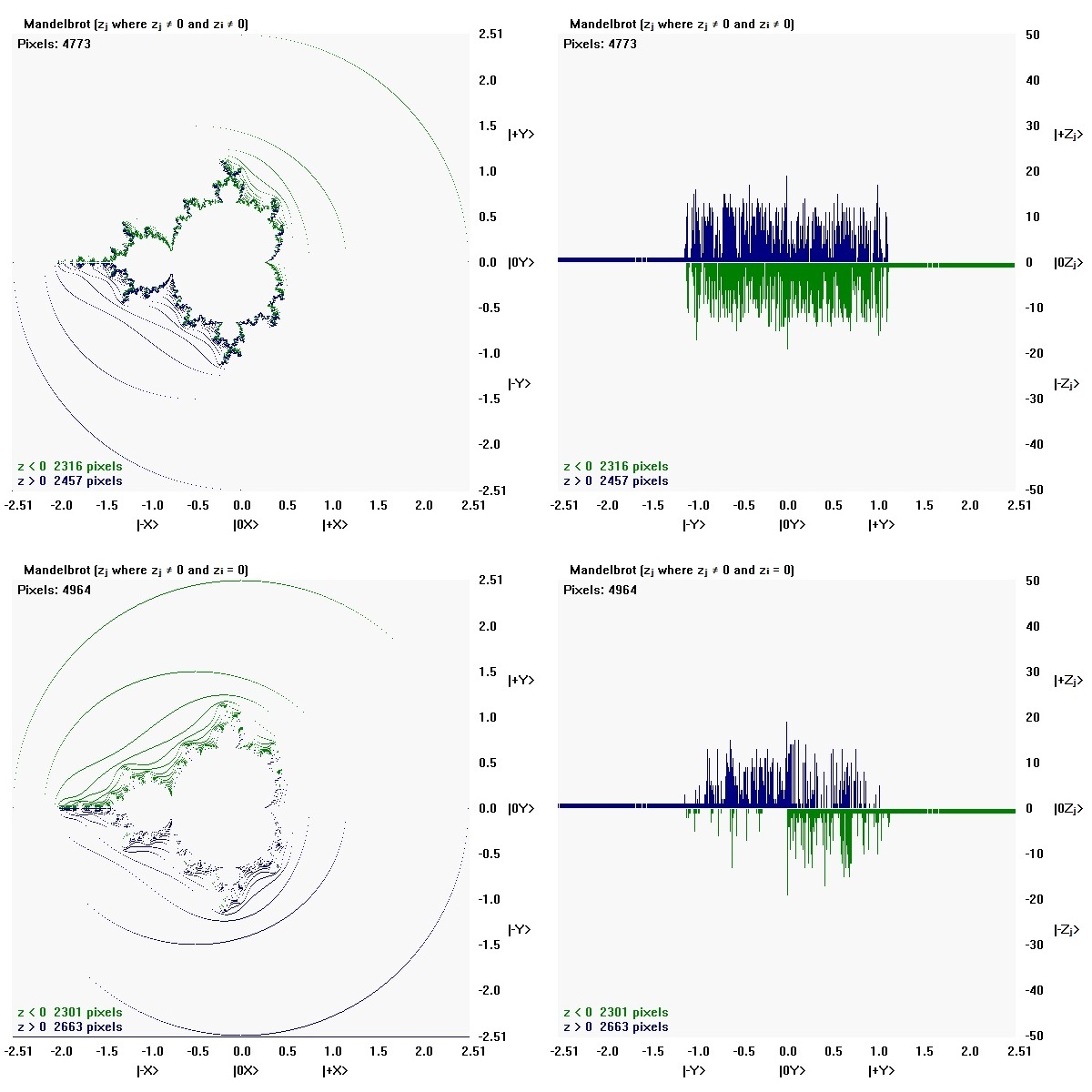
Mandelbrot (zⱼ where zⱼ ≠ 0 and zᵢ = 0)
zⱼ reflects points found only in the y-direction. There are 4964 zⱼ pixels.

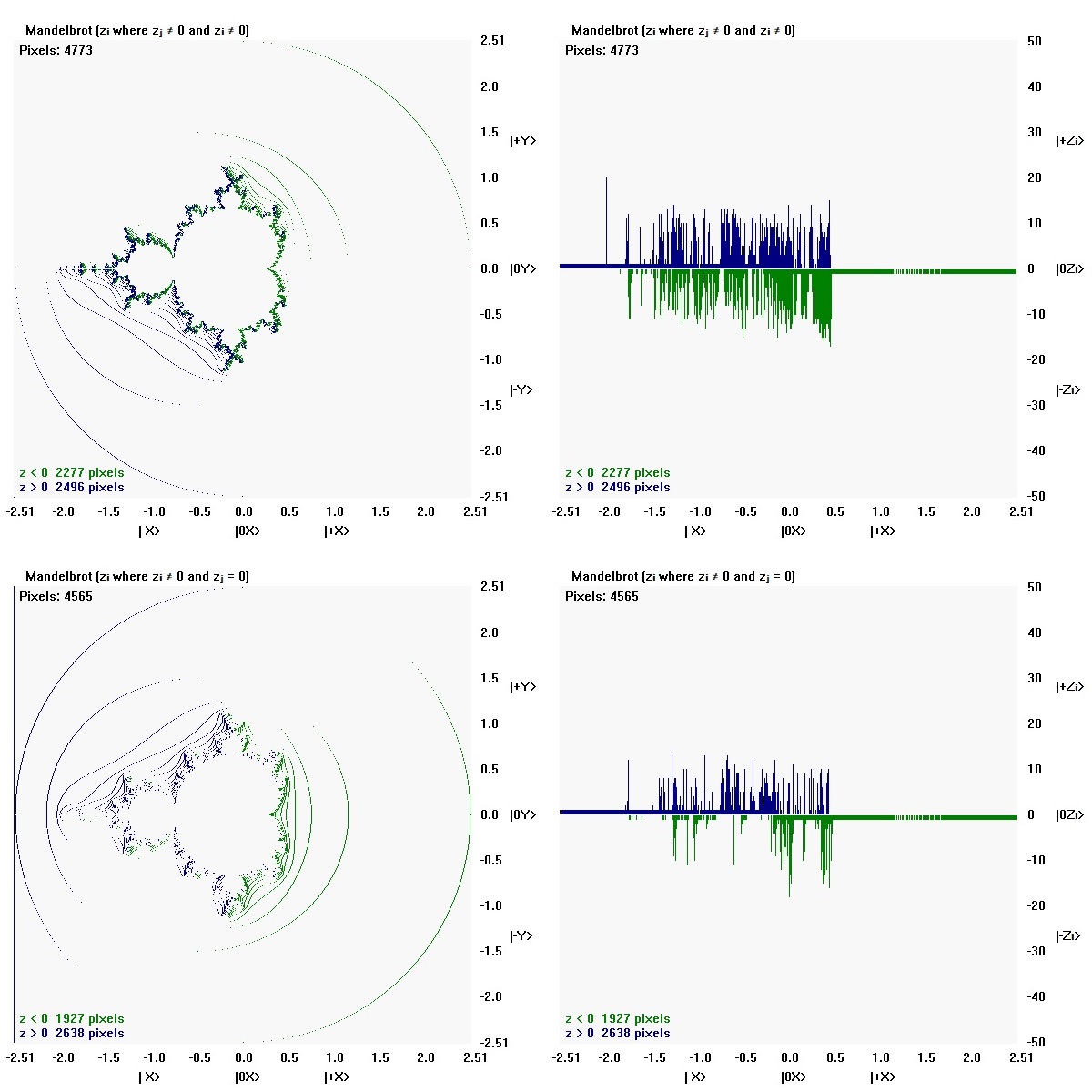
Mandelbrot (zᵢ where zᵢ ≠ 0 and zⱼ = 0)
zᵢ reflects points found only in the x-direction. There are 4565 zᵢ pixels.

Mandelbrot (zⱼ ≠ 0 and zᵢ ≠ 0)
zⱼ ≠ 0 and zᵢ ≠ 0 reflect points in common in both the x-direction and the y-direction.
The points may be common to both zⱼ and zᵢ, but the state values are different.
There are 4773 zⱼ ≠ 0 and zᵢ ≠ 0 pixels.

To obtain the complete map, zⱼ ≠ 0, zᵢ ≠ 0 are summed yielding the map seen to the right:

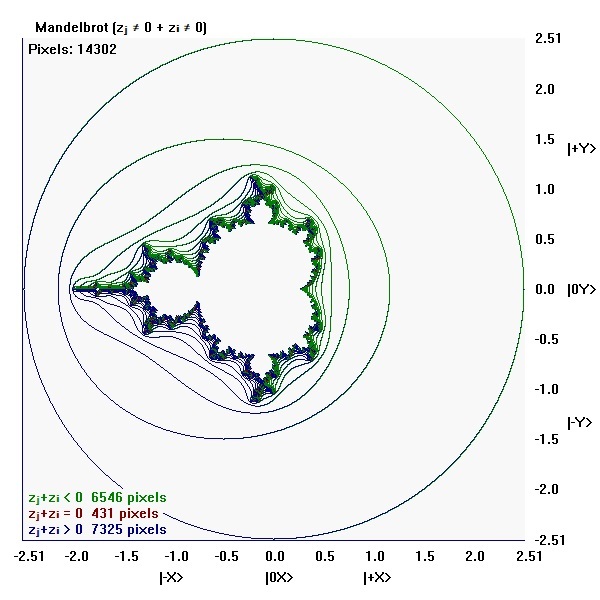
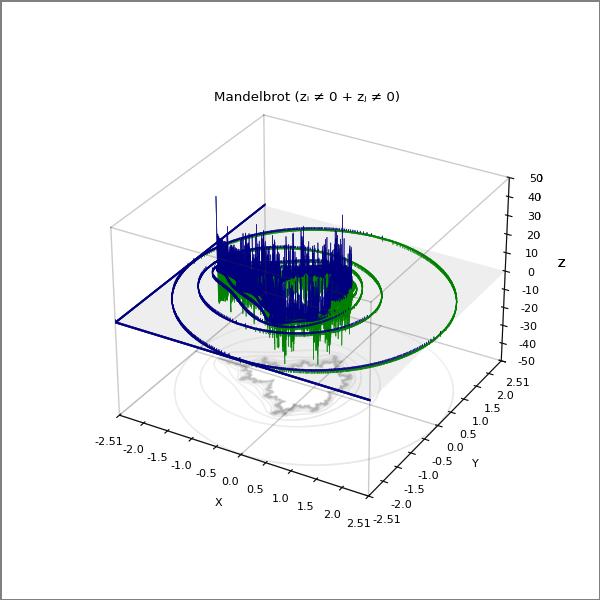
Mandelbrot (zⱼ ≠ 0 + zᵢ ≠ 0)
There are 253009 pixels in the map, but only 14302 pixels where either zⱼ ≠ 0 or zᵢ ≠ 0 or both zⱼ ≠ 0, zᵢ ≠ 0.
There are 431 pixels where zⱼ ≠ 0 and zᵢ ≠ 0, but their sum (zⱼ ≠ 0 + zᵢ ≠ 0) = 0.
Just because you can't see it, doesn't mean it's not there.

Mandelbrot (zⱼ)

Mandelbrot State Change Totals (zⱼ) where zⱼ ≠ 0 and zᵢ = 0

Section	{-}	{0}	{+}	Sum
y1	30	0	1423	1453
y2	0	0	54	54
y3	1945	0	45	1990
y4	0	0	11	11
y5	0	0	0	0
y6	8	0	2	10
y7	1	0	1047	1048
y8	0	0	1	1
y9	317	0	80	397
Sum	2301	0	2663	4964

Mandelbrot State Change Totals (zⱼ) where zⱼ ≠ 0 and zᵢ ≠ 0

Section	{-}	{0}	{+}	Sum
y1	352	0	1688	2040
y2	0	0	2	2
y3	971	0	337	1308
y4	8	0	15	23
y5	0	0	0	0
y6	17	0	6	23
y7	232	0	253	485
y8	3	0	0	3
y9	733	0	156	889
Sum	2316	0	2457	4773